Theory
In music, 22 equal temperament, called 22-tet, 22-edo, or 22-et, is the scale derived by dividing the octave into 22 equally large steps. Each step represents a frequency ratio of the twenty-second root of 2, or 54.55 cents. Because it distinguishes 10/9 and 9/8, it’s good for 5-limit.
The idea of dividing the octave into 22 steps of equal size seems to have originated with nineteenth century music theorist RHM Bosanquet. Inspired by the division of the octave into 22 unequal parts in the music theory of India, Bosenquet noted that such an equal division was capable of representing 5-limit music with tolerable accuracy. In this he was followed in the twentieth century by theorist José Würschmidt, who noted it as a possible next step after 19 equal temperament, and J. Murray Barbour in his classic survey of tuning history, ”Tuning and Temperament”.
The 22-et system is in fact the third equal division, after 12 and 19, which is capable of approximating the 5-limit to within a TE error of 4 cents/oct. While not an integral or gap edo it at least qualifies as a zeta peak. Moreover, there is more to it than just the 5-limit; unlike 12 or 19 it is able to approximate the 7- and 11-limits to within 3 cents/oct of error. While 31 equal temperament does much better, 22-et still allows the use of these higher-limit harmonies, and in fact 22 is the smallest equal division to represent the 11-limit consistently. Furthermore, 22-et, unlike 12 and 19, is not a meantone system. The net effect is that 22 allows, and to some extent even forces, the exploration of less familiar musical territory, yet is small enough that it can be used in live performances with suitably designed instruments, such as 22-tone guitars and the like.
22-et can also be treated as adding harmonics 3 and 5 to 11-EDO’s 2.7.9.11.15.17 subgroup, making it a (rather accurate) 2.3.5.7.11.17 subgroup temperament. Let us also mind it’s approximation of the 31st harmonic is within half a cent, which is fairly accurate. It also approximates some intervals involving the 29th harmonic well, especially 29/24, which is also matched within half a cent. This leaves us with 2.3.5.7.11.17.29.31.
22-et is very close to an extended “quarter-comma superpyth”, a tuning analogous to quarter-comma meantone except that it tempers out the septimal comma 64:63 instead of the syntonic comma 81:80. Because of this it has nearly pure septimal major thirds (9:7).
Intervalic Naming Systems
The intervals of 22 EDO may be thought of as a system arising from both Superpyth and Porcupine temperament therefore, it makes sense to categorize each on as major and minor of each temperament. s indicates superpyth, p indicates Porcupine, because p now represents procupine and not perfect, P in perfect intervals is no longer used in this system. Instead the number is used without P and is read as either just the number or “Natural”. Example: P5 becomes 5 or N5 = Perfect fifth becomes Natural fifth.
Properties of 22 equal temperament
Possibly the most striking characteristic of 22-et to those not used to it is that it does not “temper out” the syntonic comma of 81/80, and therefore is not a system of meantone temperament. This means that 22 distinguishes a number of Pythagorean and 5-limit intervals that 12-EDO, 19-EDO, 31-EDO, … do not distinguish, such as the two whole tones 9/8 and 10/9. Indeed, these distinctions are exaggerated in comparison to 5-limit JI and many more accurate temperaments such as 34edo, 41edo and 53edo.
The diatonic scale it produces is instead derived from superpyth temperament, which despite having the same melodic structure as meantone’s diatonic scale (LLsLLLs or, 5L 2s), has thirds approximating 9/7 and 7/6, rather than 5/4 and 6/5. This means that the septimal comma of 64/63 vanishes, rather than the syntonic comma of 81/80, which is one of the core features of 22-EDO. Superpyth is melodically interesting for having a quasi-equal pentatonic scale (as the large whole tone and subminor third are rather close in size) and a more uneven heptatonic scale, as compared with 12-equal and meantone systems: step patterns 4 4 5 4 5 and 4 4 1 4 4 4 1, respectively.
It additionally tempers out the porcupine comma or maximal diesis of 250/243, which means that 22-EDO supports porcupine temperament. The generator for porcupine is is a flat minor whole tone of 10/9, two of which is a slightly sharp 6/5, and three of which is a slightly flat 4/3, implying the existence of an equal-step tetrachord, which is characteristic of Porcupine. Porcupine is notable for being the 5-limit temperament lowest in badness which is not approximated by the familiar 12-tone equal temperament, and as such represents one excellent point of departure for examining the harmonic properties of 22-EDO. It forms MOS’s of 7 and 8, which in 22-EDO are tuned respectively as 4 3 3 3 3 3 3 and 3 1 3 3 3 3 3 3 (and their respective modes).
The 164¢ “flat minor whole tone” is a key interval in 22-EDO, in part because it functions as no less than three different consonant ratios in the 11-limit: 10/9, 11/10, and 12/11. It is thus extremely ambiguous and flexible. The trade-off is that it is very much in the cracks of the 12-equal piano, and so for most 12-equal listeners, it takes some getting used to. Simple translations of 5-limit music into 22-EDO can sound very different, with a more complex harmonic quality inevitably arising. 22edo does not contain a neutral third but both the 5-limit thirds have a “neutral-like” quality since they are tempered closer together rather than farther apart as in 12edo.
22-EDO also supports Orwell temperament, which uses the septimal subminor third as a generator (5 degrees) and forms MOS scales with step patterns 3 2 3 2 3 2 3 2 2 and 1 2 2 1 2 2 1 2 2 1 2 2 2. Harmonically, Orwell can be tuned more accurately in other temperaments, such as 31edo, 53edo and 84edo. But 22-equal Orwell has a leg-up on the others melodically, as the large and small steps of Orwell[9] are easier to distinguish in 22.
Other 5-limit commas 22-EDO tempers out include the diaschisma, 2048/2025 and the magic comma or small diesis, 3125/3072. In a diaschismic system, such as 12-et or 22-et, the diatonic tritone 45/32, which is a major third above a major whole tone representing 9/8, is equated to its inverted form, 64/45. That the magic comma is tempered out means that 22-et is a magic system, where five major thirds make up a perfect fifth.
In the 7-limit 22-et tempers out certain commas also tempered out by 12-et; this relates 12 equal to 22 in a way different from the way in which meantone systems are akin to it. Both 50/49, (the jubilee comma), and 64/63, (the septimal comma), are tempered out in both systems. Hence because of 50/49 they both equate the two septimal tritones of 7/5 and 10/7, and because of 64/63 they both do not distinguish between a dominant seventh chord and an otonal tetrad. Hence both also temper out (50/49)/(64/63) = 225/224, the septimal kleisma, so that the septimal kleisma augmented triad is a chord of 22-et, as it also is of any meantone tuning. A septimal comma not tempered out by 12-et which 22-et does temper out is 1728/1715, the orwell comma; and the orwell tetrad is also a chord of 22-et.
As 22 is divisible by 11, a 22edo instrument can play any music in 11edo, in the same way that 12edo can play 6edo (the whole tone scale). 11-equal is interesting for sounding melodically very similar to 12-equal (whole steps, half steps and minor thirds in the familiar 1:2:3 ratio), but harmonically very different, in particular because it lacks perfect fifths/fourths and 5-limit major thirds/minor sixths. Similarly, 22edo is melodically similar to 24edo as both contain quarter-tones and minor, neutral, and major seconds; but 22edo offers much better all-around harmonies than 24. In Sagittal, 11 can be notated as every other note of 22.
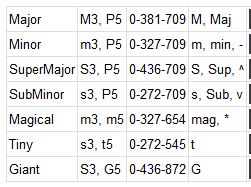
Triads
22 EDO contains many possibilities for triads, this list is by no means an exhaustive one, but it highlights some common and interesting one’s.
Seventh Chords
While triads show promise, the real fun is tetrads in 22 EDO. There are a wealth of interesting sonorities by a variety of four note tertian based chords.
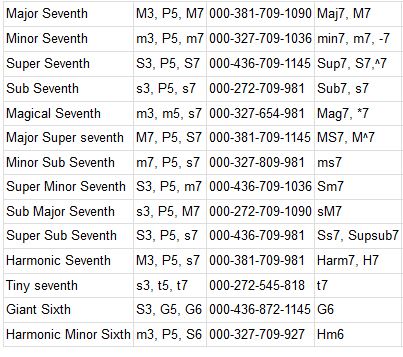
right click and select view to see the full image

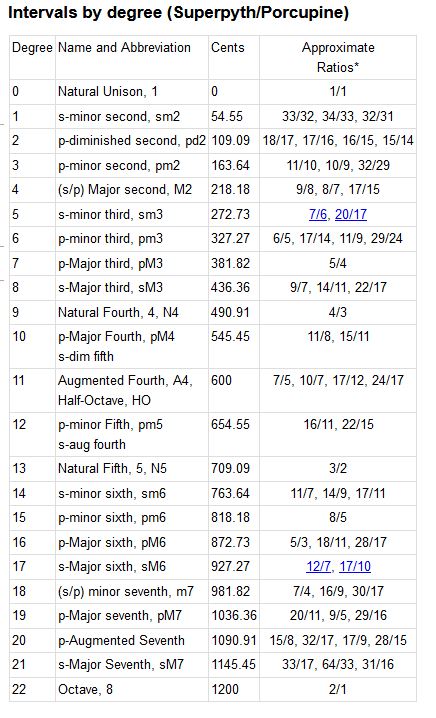
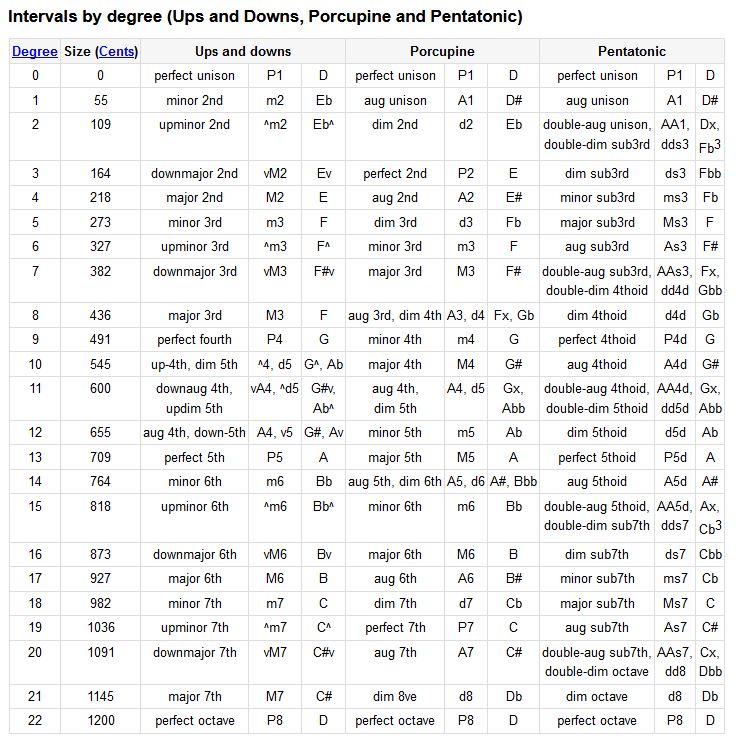

Taken from the xenharmonic wiki to preserve some knowledge