Bohlen-Pierce
The Bohlen-Pierce (BP) scale is a nonoctave scale, a 13-part equal division of the perfect-twelfth (3/1) or Tritave (13edt). Each step is about 146 ¢, making it a macrotonal scale. It is closely related to the rank two temperament bohpier. Bohlen-Pierce is normally thought of (if not in these terms, then in fact) as a temperament defined on the 3.5.7 subgroup. However, it (or at least 3.5.7-limit 13edt) can be extended to the 3.5.7.11/4 subgroup. This extension is controversial because of the presence of 2 in the denominator of 11/4, but the interval is present in the sense that 3^(12\13) provides an approximation to it. Chords of Bohlen-Pierce, from this extended perspective, may be found listed on the page chords of bohpier. Bohlen-Pierce was discovered independently by Heinz Bohlen, John Pierce, Kees van Prooijen, and perhaps others, usually noticed for its good approximation of odd-number just ratios 3:5, 5:7, 3:7, etc.; but not necessarily 4:11, 5:6, 6:7, etc.
My The Bohlen-Pierce guitar

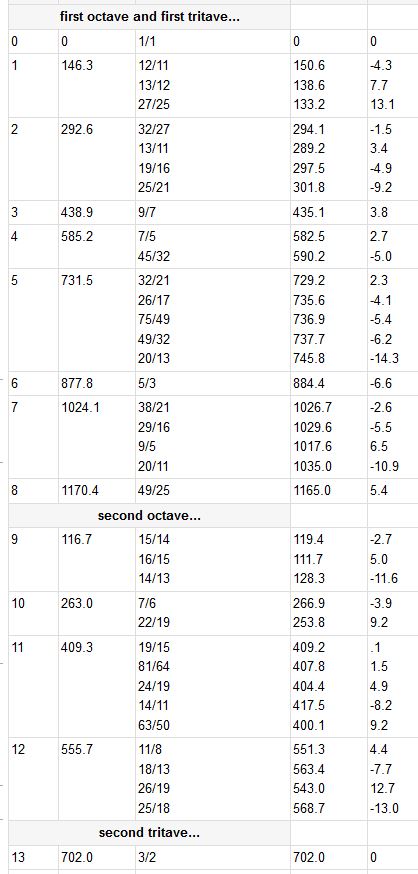
Intervals of BP
degree cents value nearby frequency ratios cents value difference between BP interval & just interval
EDTs compatible with the BP nonatonic scale
The Lambda MOS family of 4L+5s is well known for accurately representing the 3.5.7 subgroup when the generator is near the boundary of propriety, such as in the case of the Bohlen Pierce scale. Below is a list of the equal-temperaments which contain a 4L+5s scale using generators between 422.7 cents and 475.5 cents.
L=1 s=0 4 edt
L=1 s=1 9 edt (5flat40 7sharp18)
L=2 s=1 13 (5flat7 7flat3)
L=3 s=1 17 (5sharp10 7flat12)
L=3 s=2 22 (~14edo)
L=4 s=1 21
L=4 s=3 31
L=5 s=1 25
L=5 s=2 30 (~19edo) (5sharp3 7flat8)
L=5 s=3 35 (~22edo) (5flat14 7sharp0)
L=5 s=4 40
L=6 s=1 29
L=6 s=5 49 (~31EDO) (5sharp8 7sharp8) (Schism*)
L=7 s=1 33
L=7 s=2 38 (~24edo)
L=7 s=3 43 (~27edo) (5sharp0 7flat6)
L=7 s=4 48 (5flat13 7flat0)
L=7 s=5 53
L=7 s=6 58 5sharp1 7sharp10 (Schism*)
*Schism, by which I mean, the most accurate value for 5/3 and-or 7/3 is found outside the 4L+5s MOS.
[Also, the way I see it, as 4edt and 9edt are comparable to 5edo and 7edo, then the “counterparts” of Blackwood and Whitewood would be found in multiples therein and would be octatonic and octadecatonic, eg. 12edt and 27edt.]
Taken from the xenharmonic wiki to preserve some knowledge