17-EDO divides the octave in 17 equal steps, each 70.588 cents in size. It is the seventh prime edo, following 13edo and coming before 19edo.
An introduction to 17-EDO theory
17-EDO can plausibly be treated as a 2.3.25.7.11.13.23 subgroup temperament, for which it is quite accurate (though the 7-limit ratios are generally not as well-represented as those of the other integers). Because the 3, 7, 11, and 13 are all sharp, it adapts well to octave shrinking; 27edt (a variant of 17edo in which the octaves are flattened by ~2.5 cents) is a good alternative. Another one is 44ed6.
As a no-fives system, it is best used with timbres in which harmonic multiples of 5 are attenuated or absent. Also, the standard major chord (4:5:6) cannot be used since it includes the fifth harmonic.
Instead, the tonic chords of 17-EDO could be considered to be the tetrad 6:7:8:9 and its utonal inversion, the former of which is a subminor chord with added fourth, and the latter a supermajor chord with added second (resembling the famous mu major chord of Steely Dan fame). These are realized in 17-EDO as 0-4-7-10 and 0-3-6-10, respectively. Both of these have distinct moods, and are stable and consonant, if somewhat more sophisticated than their classic 5-limit counterparts. To this group we could also add the 0-3-7-10 (which is a sus4 with added second, or sus2 with added fourth). These three chords comprise the three ways to divide the 17-EDO perfect fifth into two whole tones and one subminor third. Chromatic alterations of them also exist, for example, the 0-3-7-10 chord may be altered to 0-2-7-10 (which approximates 12:13:16:18) or 0-3-8-10 (which approximates 8:9:11:12). The 0-3-8-10 chord is impressive-sounding, resembling a sus4 but with even more tension; it resolves quite nicely to 0-3-6-10.
right click and select view image to see full size
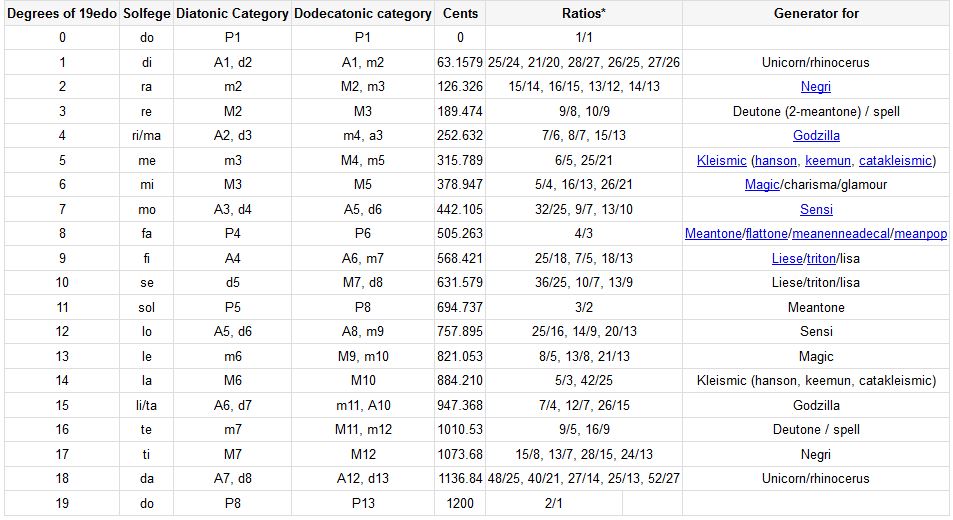
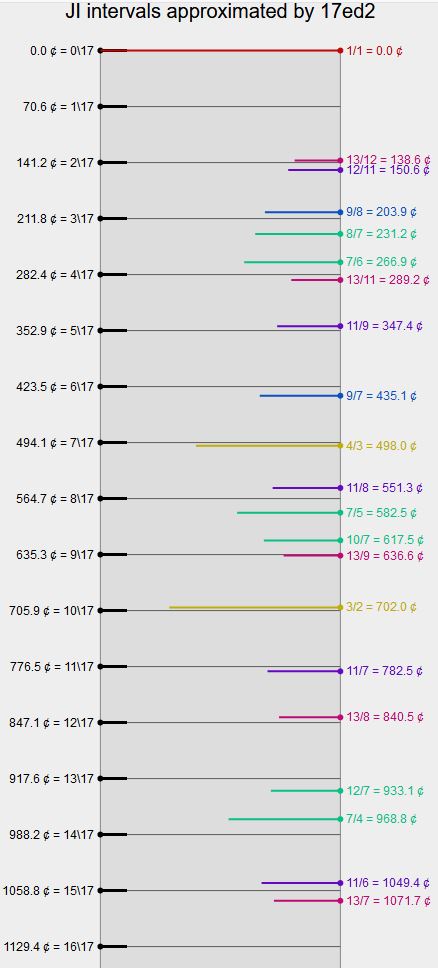
Taken from the xenharmonic wiki to preserve some knowledge
Music by me in this tuning
and some 17 edo theory